3D变换
3D变换包含四种基本变换:平移(translation)、旋转(ratation)、缩放(scale)、和透视(perspective).这四种基本变换联合决定了在一个新坐标系中的么一个定点位置是怎么转换为参考坐标系中的一个位置的。
每个基本变换对应于矩阵的一个简单变化。定义一个与参考系相同的坐标系叫做单位矩阵(identity matrix).任意两个矩阵在一个级联(concatenation) 操作中结合产生一个新矩阵,这个新矩阵包含了两个矩阵的所有变换。实际上每个基本变换会产生一个简单的矩阵,然后把这个简单的矩阵与当前变换矩阵连接起来产生一个新的当前矩阵。
“矩阵级联” 又称为”矩阵乘法”(matrix muliplication)。注意:矩阵乘法不满足乘法交换律。
1、平移
沿着某一个方向移动,平移通常不影响坐标做的的单位长度,也不会对坐标轴的方向做出改变。GLKit提供了GLKMatrix4MakeTranslation(float x,float y,float z)函数。这个函数通过平移一个单位矩阵来返回一个定义了坐标系的新矩阵。
2、旋转
旋转是通过相对参考坐标系坐标轴的方向旋转新坐标系的坐标轴来定义一个新坐标系。GLKit提供了GLKMatrix4MakeRotation(float angleRadians,float x,float y,float z)函数。这个函数通过旋转一个单位矩阵来返回定义了一个坐标系的新矩阵。angleRadians参数制定了要旋转的弧度数。使用GLKMathDegreesToRadians()函数可以把角度转换成弧度。
3、缩放
缩放是通过相对于参考系的坐标轴的单位长度改变新坐标系的坐标轴的单位长度来定义一个新坐标系。缩放的坐标系与参考坐标系使用统一远点,坐标轴的方向不会改变。不过,通过一个复制所做的缩放会翻转坐标轴的方向。GLKIt 提供了GLKMatrix4MakeScale(float x,float y,float z)函数,这个函数会通过扩大或者缩小一个单位矩阵的任意坐标轴的单位长度来返回一个定义了坐标系的矩阵
4、透视
透视是通过相对于参考坐标系的坐标轴的单位长度多样化新坐标系的坐标轴的单位长度来定义一个新的坐标系,透视不会改变坐标轴 的方向或者远点。透视会产生一个金大元小的效果。GLKit 提供了GLKMatrix4MakeFrustum(float left,float right,float bottom,float top, float nearVal,float farVal)函数,这个函数会透视一个单位矩阵来返回一个定义了坐标系的新矩阵,透视坐标系的形状类似一个角锥体的平截头体。
4中基本变换可以定义新的坐标系,不过需要注意的是变换的顺序。不同的顺序变换有着天壤之别。在我们的demo中,矩阵的顺序基本上是不变的。总是 投影矩阵 × 视图矩阵 × 模型矩阵 × 3D位置这个顺序。具体更详细的请参看白云飘飘或者OpenGL ES 开发指南。
透视和平截头体
OpenGL ES 使用一个叫做视域(viewing volume) 的几何体来决定一个场景的哪些片元将会显示在最终的渲染结果中。处于视域范围之外的几何图形会被剔除(clipped),这意味着它会被丢弃。视域有时也被称为投影(projection).
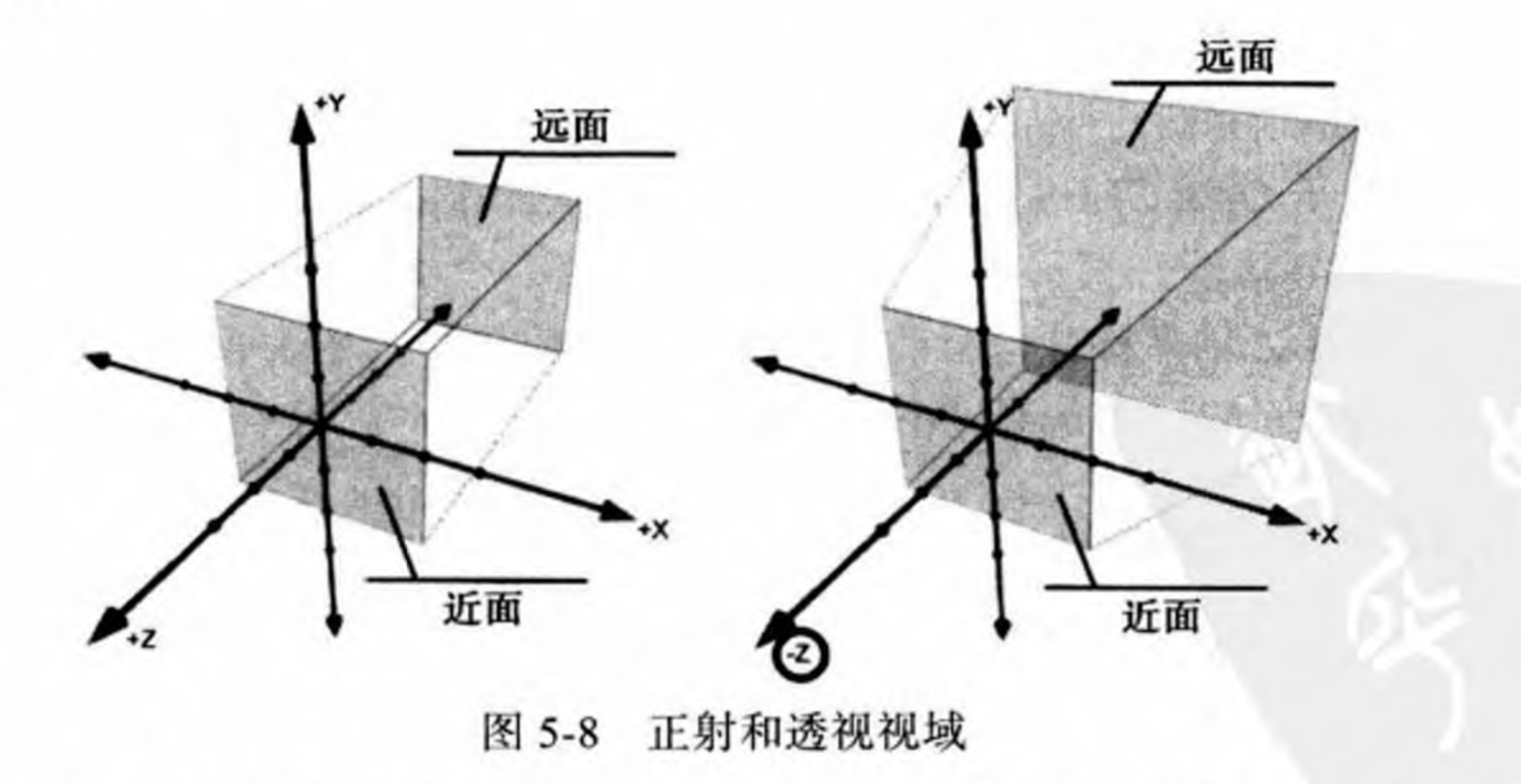
一个立方体或者矩形视域叫做一个正射投影(orthographic projection)。利用一个正射投影,视点与每个位置之间的距离对于投影毫无影响。GLKit 的GLKMatrix4MakeOrtho(GLfloat left,GLfloat right,GLfloat bottom,GLfloat top,GLFloat near,GLfloat far)函数会返回一个矩阵,这个矩阵定义了一个由left、right、bottom、top、near、far、所界定的矩形视域。
当使用透视投影(perspective projection)时,视域不再是矩形。变成了角锥体被窃取顶端之后的形状—平截头体,如图:当投影到2D像素颜色渲染缓存中后,离视点越远的对象越小,月就是呈现近大远小的现象。GLKIT 的GLKMatrix4MakeFrustum 函数重新定义一个新矩阵。这个矩阵通常会与当前projectionMatrix级联来定义视域。
最后,总结一下,这一节主要讲的3D 变换,讲的一些概念。具体的实践在demo 中会有体现。
最后,留一个思考题,为什么物体会呈现出近大远小的现象。

最后,附上我自己在学习过程中的源码:
参考:
[1]:OpenGL ES 应用开发实践指南iOS卷