在做了将近一年的逆向开发后,发现自己基础很薄若,有一次,老大让实现一个类似Linux 的目录树的机构,自己居然还得去请教老大(O__O “…这些数据结构上都有的,暴露了🙂)。著名计算机科学家沃斯(Nikikaus Wirth)定义程序为:程序=数据结构+算法。算法是灵魂,数据结构是加工对象,语言是工具。还是从最基础的学起吧。
栈与队列
在算法导论中是这样定义的:栈和队列都是动态集合,且在其上进行delete操作所移除的元素都是预先设定的。在栈(stack)中,被删除的是最近插入的元素:栈实现的是一种后进先出(last-in,first-out,LIFO)的策略。类似地,在队列(queue)中,被删去的总是在集合中存在时间最长的那个元素:队列实现的是一种先进先出(first-in,first-out,FIFO)策略。在计算机上实现基本有两种方式:数组与链表。
栈
栈又叫LIFO(后进先出)表。栈上的insert操作称为压栈(push),而delete操作称为出栈(pop)。栈的操作只能在一个位置上进行,该位置是表的末端,称之为top(栈顶)。在生活中,我们上下电梯,就是栈的最好例子。在桶子里装鸡蛋,都是栈。因为只有最上边的最后进入,最先出来。我们可以用几行伪代码来实现。
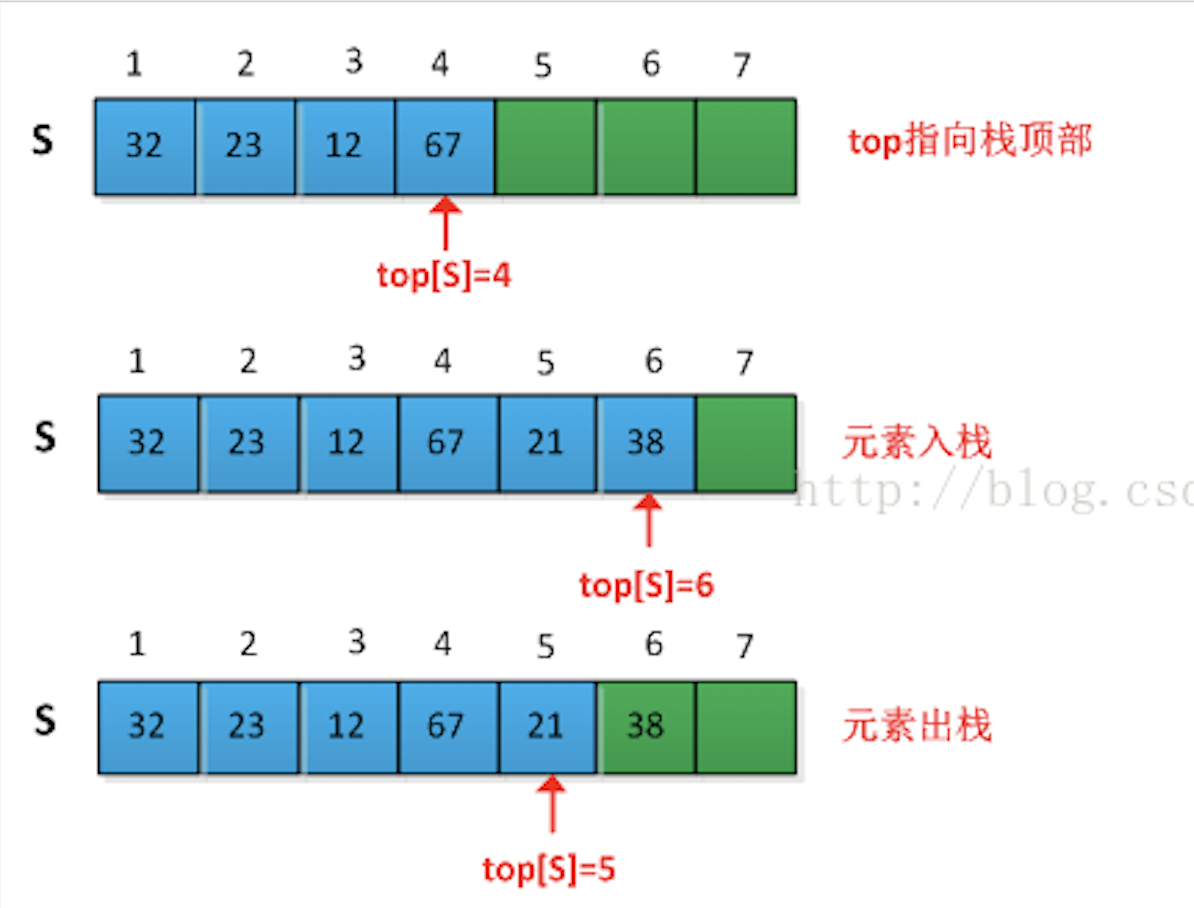
图片来自于网上
如图所示,可以用一个数组S[1..n] 来实现一个最多可容纳n个元素的栈,该数组有一个属性S.top,指向最新插入的元素,栈中包含的元素为S[1..S.top],其中S[1]是栈底元素,而S[S.top]是栈顶元素,那么栈的集中操作只需要几行代码就可以搞定:
STACK_EMPTY(S)
if S.top == 0
return TRUE
else
return FALSE
PUSH(S)
S.top = S.top + 1
S.[S.top] = x
POP(S)
if SRACK_EMPTY(S)
ERROR "underflow"
else S.top = S.top - 1
return S[S.top + 1]
当然这只是伪代码,有时候我们只需要弄清楚它的原理,没有必要写一大堆代码出来,就可以使用伪代码来说明,这是一个号的习惯,值得我们学习,我也是在学习。下面我们就来看看栈的具体实现及实际应用:
栈的链表实现
定义
//链表节点的定义
typedef struct _Node {
int data;
struct _Node *pNext;
}StackNode;
//定义栈顶指针
typedef struct _Stack {
int count;
StackNode *top;
}Stack;
//初始化栈
void InitStack(Stack *stack);
//push 入栈
void PushStack(Stack *stack,int data);
//pop 出栈
int PopStack(Stack *stack);
//判断栈是否为空
int IsEmptyStack(Stack *stack);
//获取栈顶元素
int GetTopStack(Stack *stack);
//最后销毁栈
void DestroyStack(Stack *stack);
栈的实现还是蛮容易的,没什么好说的
#include "Stack.h"
void InitStack(Stack *stack) {
stack = malloc(sizeof(Stack));
if (NULL == stack) {
return;
}
stack->count = 0;
stack->top = NULL;
}
void PushStack(Stack *stack,int data) {
StackNode *p_new = malloc(sizeof(StackNode));
if (p_new == NULL) {
perror("malloc failed!!");
exit(EXIT_FAILURE);
}
p_new->data = data;
p_new->pNext = stack->top;
stack->top = p_new;
stack->count += 1;
}
int PopStack(Stack *stack) {
StackNode *p_delete = stack->top;
if (IsEmptyStack(stack)) {
printf("this stack is empty!!\n");
// exit(EXIT_FAILURE);
return 0;
}
int data = p_delete->data;
stack->top = p_delete->pNext;
stack->count -= 1;
free(p_delete);
p_delete = NULL;
return data;
}
int IsEmptyStack(Stack *stack) {
if (stack->top != NULL) {
return 0;
}
return 1;
}
int GetTopStack(Stack *stack) {
if (IsEmptyStack(stack)) {
return -1;
}
return stack->top->data;
}
void DestroyStack(Stack *stack) {
StackNode *pNode = NULL;
while (stack->top != NULL) {
pNode = stack->top;
stack->top = pNode->pNext;
stack->count -= 1;
free(pNode);
pNode = NULL;
}
}
具体的应用最经典的便是四则运算了,我也实现了一个,项目很小,我就不往GitHub上提交了;平时iOS开发push 页面时就是一个栈的典型应用。接下来就来看看队列。
队列
像栈一样,队列(queue)也是表。但不同的是,它遵循先进先出(FIFO)的原则,因此,队列的插入在一端进行而删除在另一端。队列的基本操作是入队,在队的末尾插入一个元素。删除一个元素叫出队,必须在队头(front)进行删除。同样,我们来看图:

如图,数组Q[1..n] 来实现一个最多容纳n-1个元素的队列的一种方式,该队列有一个属性Q.head 指向队头的元素,而属性Q.tail 则指向下一个元素将要插入的位置。在队列的操作中,我们要特别注意避免上溢和下溢的发生。
下面给出队列enqueue(入队)和dequeue(出队)的伪代码,假设n = Q.length.
ENQUEUE(Q,x)
Q[Q.tail] = x
if Q.tail == Q.length
Q.tail = 1
else Q.tail = Q.head + 1
DEQUEUE(Q)
x = Q[Q.head]
if Q.head == Q.length
Q.head = 1
else Q.head = Q.head + 1
return x
纠结了好长时间,要不要贴个队列的实现代码出来,还是贴出来吧
#ifndef Queue_h
#define Queue_h
#include <stdio.h>
typedef struct _qNode{
int data;
struct _qNode *next;
}QNode;
typedef struct _Queue {
struct _qNode *head;
struct _qNode *tail;
}Queue;
void initQueue(Queue *queue);
int enqueue(Queue *queue,int data);
int dequeue(Queue *queue);
int isEmpty(Queue *queue);
void destoryQueue(Queue *queue);
#endif /* Queue_h */
#include "Queue.h"
#include <stdlib.h>
#include <string.h>
void initQueue(Queue *queue) {
queue = malloc(sizeof(Queue));
if (NULL == queue) {
perror("init queue failed!!");
return;
}
memset(queue,0,sizeof(Queue));
queue->head = queue->tail = NULL;
}
int enqueue(Queue *queue,int data) {
if (NULL == queue) {
return -1;
}
QNode *node = malloc(sizeof(QNode));
memset(node, 0, sizeof(Queue));
node->data = data;
node->next = NULL;
if (queue->head == NULL) {
queue->head = queue->tail = node;
return 0;
}
queue->tail->next = node;
queue->tail = queue->tail->next;
return 0;
}
int dequeue(Queue *queue) {
if (NULL == queue) {
return -1;
}
if (isEmpty(queue)) {
return -1;
}
QNode *qNode = queue->head;
int data = qNode->data;
if (queue->tail == qNode) {
free(queue);
queue->tail = NULL;
}
queue->head = queue->head->next;
free(qNode);
qNode = NULL;
return data;
}
int isEmpty(Queue *queue) {
if (NULL == queue) {
return 1;
}
if (queue->head == NULL) {
return 1;
}
return 0;
}
void destoryQueue(Queue *queue) {
while (queue->head != NULL) {
QNode *node = queue->head;
queue->head = queue->head->next;
free(node);
node = NULL;
}
queue = NULL;
free(queue);
}
d队列的应用
队列的应用在生活中随处可见,我们排队买票,就是一个队列;打印机作业就是一个队列;当然还有很多其他丰富的用途。
总结
栈和队列是数据结构算法中非常基础的东西,是更加深入的学习的基础,理解这些过程非常重要。当然数据结构中还有表(ADT),与栈和队列构成最基本的三种数据结构。很基础,极容易理解,就不浪费时间了。